Also question is, what are the four input components of the aggregate production function when GDP is the output?
Factors of production are inputs used to produce an output, or goods and services. They are resources a company requires to attempt to generate a profit by producing goods and services. Factors of production are divided into four categories: land, labor, capital and entrepreneurship.
Subsequently, question is, how do you calculate aggregate production function? Use the Cobb-Douglas function to determine total aggregate production. The formula is given as production is equal to real output per input unit (sometimes simplified to "technology") times labor input times capital input or Y = A X L^a X K^b.
Correspondingly, what is the aggregate production function?
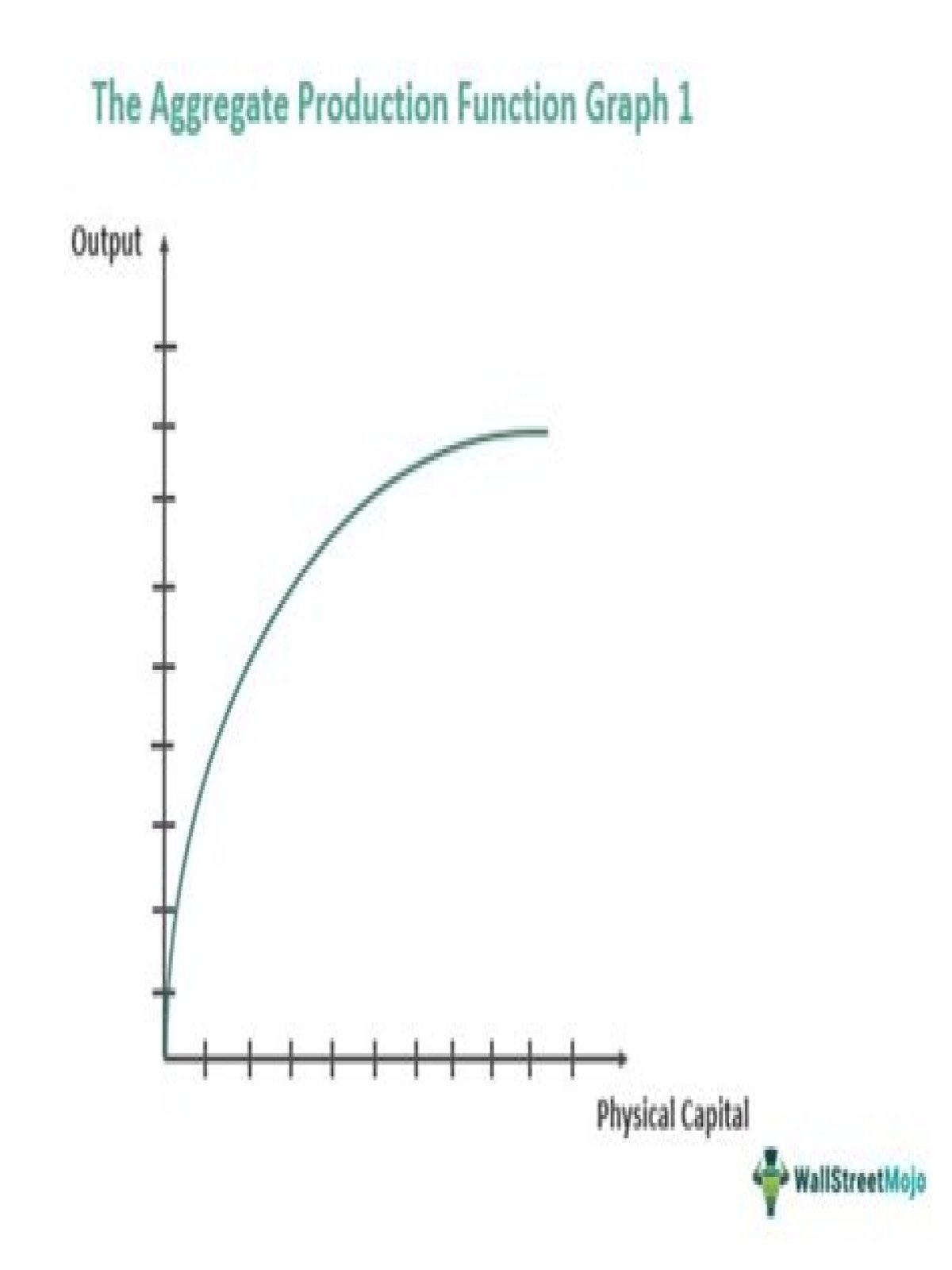
The aggregate production function describes how total real gross domestic product (real GDP) in an economy depends on available inputs. Aggregate output (real GDP) depends on the following: Physical capital—machines, production facilities, and so forth that are used in production.
What happens to GDP when the input increases?
If there are more workers in an economy, or if they work longer hours, the economy will produce more real GDP. With more education and skills, we can produce more output. Of course, this input more often decreases rather than increases over time, as economies use up their existing stocks of natural resources.
What is F in the production function?
How do you measure productivity?
What are the three major components of economic growth?
How does technology affect GDP?
Is physical capital included in GDP?
What happens when GDP goes down?
Why is labor productivity important?
What is the relationship between aggregate income and aggregate production?
What are the types of production function?
- A production function may be expressed in three forms:
- (A) Increasing Production Function:
- (ii) Increasing production function with increasing marginal returns on the variable input:
- (iii) Increasing production function with decreasing marginal returns to the variable factor:
- (B) Decreasing Production Function: